The Fibonacci Sequence & the Golden Ratio
The Fibonacci sequence is a series of numbers produced through taking consequecutive sums starting with 0 and 1.
- 0 + 1 = 1
- 1 + 1 = 2
- 1 + 2 = 3
- 2 + 3 = 5
- 3 + 5 = 8
- and so on...
The Fibonacci sequence has a close relationship with the golden ratio, an irrational number which approximates to 1.618 and is represented by the Greek symbol φ (phi). If you take the ratio between two consecutive Fibonacci numbers, it becomes an increasingly accurate approximation of the golden ratio. 3/2 = 1.5, 13/8 = 1.625, 89/55 = 1.61818 repeating, and it gets closer and closer the further along in the series you get.
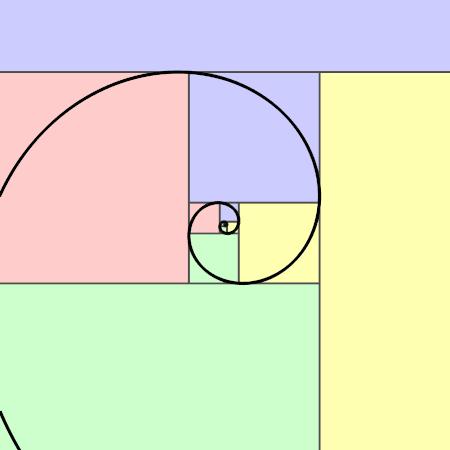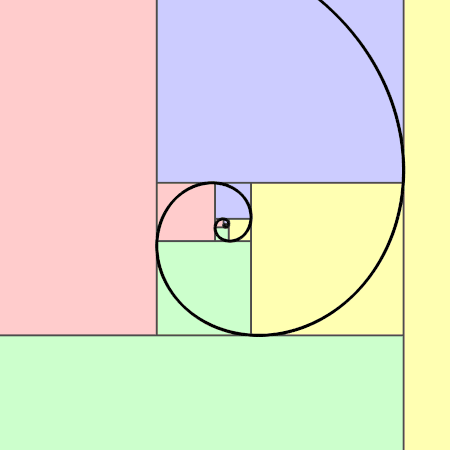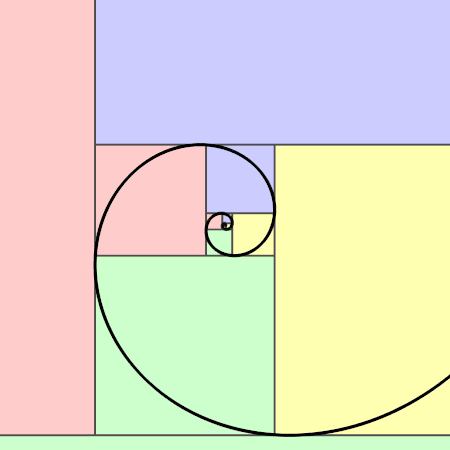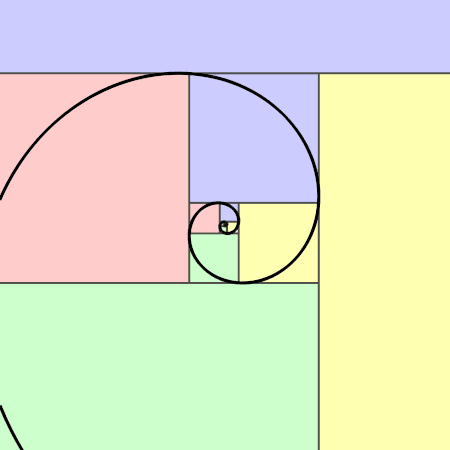
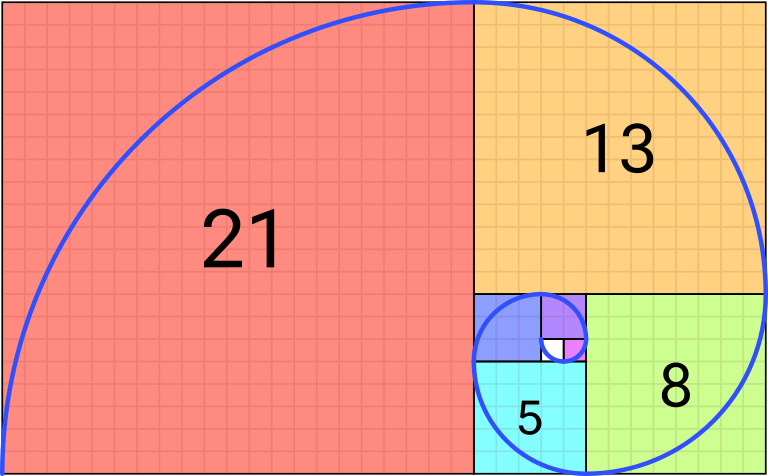
Both the Fibonacci sequence and the golden ratio can be represented visually in the form of spirals constructed of rectangles. The Fibonacci spiral begins with two squares with side length 1 which share a side. Draw a square adjacent to those with side length two. Continue spiralling around in this manner, with each square having a side length equal to a Fibonacci number. If you connect opposite corners with an arc, you achieve a lovely spiral pattern.
The golden ratio can be represented through a similar tiling process, but instead of starting from the center and working your way out, you start with the borders and work your way in. Begin with a rectangle where one side length is 1 and the other side is φ (1.618). Then, divide that rectange into a square with side length 1 and a similar "golden rectangle" with lengths ration 1:φ. Continue dividing up the remaining space until it gets too tiny to manage, and connect opposite corners with arcs as you did before.

Because of the close relationship between the Fibonacci sequence and the golden ratio, overlaying these two spirals reveals a very similar image, one which is highly reminiscent of a nautilus shell.
The presence of the series and the ratio in nature is one of the things that makes them so notable. Take any plant that arranges its seeds or leaves in spirals, like pinecones or sunflowers. If you count the number of spirals in either direction, it is very likely that the number you find is a Fibonacci number. While this may seem strange and almost magical, like evidence of intelligent design, the scientific reasoning if fairly simple.
The series and the ratio are best friends. If phi is the most irrrational number, then arranging seeds or leaves based on that ratio ensures more equitable access to growth hormones and sunlight. Of course, this isn't a hard and fast rule - there are plenty of plants that do not express Fibonacci patterns for one reason or another, but it is a shockingly common phenomenon once you are aware of it. Ever wonder why you can find plenty of 3 and 5 leaf clovers, but a 4 leaf clover is lucky?
The golden ratio is also known for its presence in art - one reason it is called the golden ratio is that it is visually appealing. For example, artists will often build the compositions of their piece according to golden rectangles or following the flow of the golden spiral to create more naturally engaging scenes.
Fractal Geometry
Coming soon!
Flexagons
Coming soon!
Higher Dimensional Geometry
Coming soon!
Gödel's Incompleteness Theorem
Coming soon!